Raffinement du langage et des arguments : la logique du premier ordre

Insuffisance de la logique propositionnelle

Considérez l’argument suivant :

1. Tous les humains sont des animaux;\
2. Certains humains sont des philosophes;\
3. Donc, certains animaux sont des philosophes.

Cet argument est valide. Pourtant, ce fait ne peut être vérifié à l’aide de la logique propositionnelle.

Quel est le problème? Donnons le dictionnaire :

• p : Tous les êtres humains sont des animaux.
• q : Certains humains sont des philosophes.
• r : Certains animaux sont des philosophes.

L’argument traduit en LP :

1. p
2. q
------
C. r

…est manifestement invalide!

La logique propositionnelle n’a pas les outils nécessaires pour justifier ce genre de situation.

Ce qui est singulier dans les énoncés :

• p : Tous les êtres humains sont des animaux.
• q : Certains humains sont des philosophes.
• r : Certains animaux sont des philosophes.

Ces expressions (« tous », « certains ») sont des quantificateurs. Ils qualifient certaines classes d’objets.

Nous y reviendrons à la fin du cours.

Autre exemple (qui n’est pas un syllogisme, avec une structure appartenant à la fois à la logique propositionnelle et à la logique du premier ordre) :

1. Si l’univers est infini, alors l’univers est la plus grande totalité;\
2. Or, s’il existe toujours pour une totalité donnée une totalité qui lui soit plus grande, alors il n’existe pas de totalité qui soit la plus grande des totalités.\
3. Alors, l’univers n’est pas la plus grande des totalités, si il est infini (conclusion partielle).\
4. Il s’ensuit que l’univers n’est pas infini (conclusion générale).

Comment traduire l’énoncé :

Il existe toujours pour une totalité donnée une totalité qui lui soit plus grande.

Il s’agit d’un énoncé logiquement complexe.

Il affirme que pour n’importe quelle totalité donnée, il en existe une autre qui lui est plus grande. En d’autres mots, pour toute totalité, il y a au moins une totalité qui est plus grande que celle qui est donnée.

Nous avons encore affaire à des quantificateurs.

Une situation

La sémantique se limite radicalement au fait que les propositions sont vraies ou fausses; ce qu’elles dénotent. La logique propositionnelle se limite aux tables de vérité.

La sémantique se rapproche beaucoup plus du langage (ce à quoi le langage réfère).

Considérons cette image :

On s’intéresse à ce qui est vrai dans toutes les situations possibles. Cela renvoie nécessairement à une infinité de cas possibles.

Pour parler d’une situation donnée, nous avons besoin :

• de moyens pour désigner les objets de cette situation (par exemple, les noms des étudiants dans la classe);
• de moyens pour caractériser ces objets et leurs relations (par exemple, qui sont les amis de qui sur Facebook, qui suit qui sur Instagram, etc.).

Pour les objets, nous devons avoir : des noms d’objets : « a », « b », « c », …

Pour les caractériser : nous avons besoin des noms de propriétés et des noms de relations :

P(-), Q(-), R(-, -).

Convention : Des lettres minuscules (a) dénotent des noms d’objets. Les lettres majuscules désignent des propriétés ou des relations. S’il n’y a qu’un tiret (-), c’est une propriété; s’il y en a deux ou plus (R(-, -)), c’est une relation.

Les ressources de Prédicat

Toutes les expressions suivantes désignent la même chose :

• Calcul des Prédicats;
• Logique des Prédicats;
• Logique du premier ordre.

Les caractérisations :

• a est Rouge;
• b est Vert;
• c est Jaune,
• etc.

En Prédicat, nous écrivons :

R(a)
V(b)
J(c)

La logique du premier ordre (monadique) utilise :

• Des symboles pour les objets : a, b, c, etc. (Ou a1, a2, a3).
• Des symboles, appelés prédicats (monadiques ou unaires) pour les propriétés de ces objets : P(-), Q(-), etc.

Comment peut-on parler de propriétés sans parler d’objets spécifiques?

• On utilise des variables x, y , z (ou x1, x2, x3, etc.)
• Ce sont des symboles du langage qui jouent le rôle de noms d’objets, mais qui n’en désignent aucun en particulier (par exemple, on ne parle pas de Jean-Jacques, mais de tous les humains possibles).

Exemples :

• P(x) dénote une propriété (« être bleu », où x est une variable et peut être remplacé à tout moment; on veut parler de la propriété, et rien d’autre).
• Q(x) dénote une propriété.

Des noms d’objets :

• a, b, c, …
• a1, a2, a3, …

Des symboles de propriétés :

• R(x) : « x est rouge »;
• V(x) : « x est vert ».

Exemples d’énoncés :

• R(a);
• V(b);
• ¬R(b) (introduction d’un connecteur propositionnel).

Lorsqu’on introduit un connecteur propositionnel (raffinement du niveau d’analyse), c’est toute l’expression qui est niée.

En Prédicat, les propriétés s’expriment à l’aide de symboles de la forme P(-), Q(-), … c’est-à-dire qu’ils ne s’attribuent qu’à un seul objet. Nous dirons que ce sont des prédicats unaires.

Les relations s’expriment à l’aide de symboles de la forme R(-, -), S(-, -, -,), T(-, -, -, -), etc. Ce sont respectivement des relations binaires, ternaires, quaternaires.

Exercice : parler en Prédicat (ou LPO)

Comment parler en Prédicat?¹

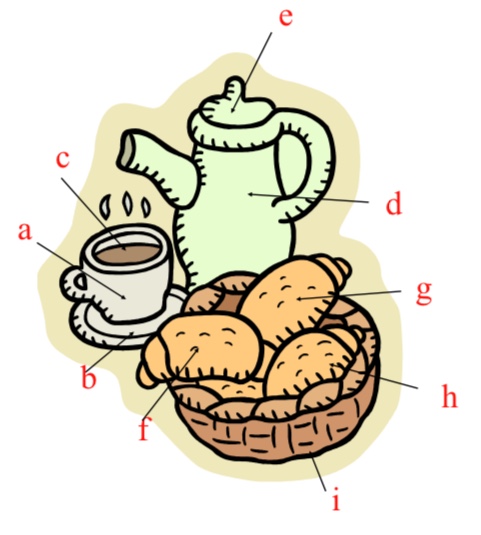
1. Faire le dictionnaire : trouver des symboles pour les objets et des symboles pour les propriétés.
2. Faire la traduction des énoncés en Prédicat.

Dictionnaire :

• T(x) : « x est une tasse »;
• C(x) : « x est un croissant ».

Énoncés (propositions) :

• T(a) := « a est une tasse »;
• C(f) := « f est un croissant »;
• C(i) := « i est un croissant ».

Dans cette situation, les deux premiers énoncés sont vrais et le dernier est faux.

Un exemple trivial

Soit l’énoncé (apprendre à faire très rapidement) :

Jean a les yeux bleus.

• Quels sont les termes?
• Quelles sont les relations impliquées?

1. Le dictionnaire :
   • j : « Jean »;
   • B(x) : « x a les yeux bleus ».
2. L’énoncé est Prédicat : B(j).

Un autre exemple

Jean est grand et Marie est intelligente.

Dictionnaire :

• j : « Jean »;
• m : « Marie »;
• G(x) : « x est grand »;
• I(x) : « x est intelligent² ».

L’énoncé en prédicat :

G(j) ∧ I(m)

On ne se sert plus des tables de vérité, mais on va se servir des arbres et de la déduction naturelle.

Généralités en Prédicat

Jusqu’à présent, le langage Prédicat ne permet que de faire référence à des faits spécifiques, particuliers. Il est impossible de donner des informations générales.

Nous pouvons dire « ce croissant est dans le panier » ou « Jean a les yeux bleus ».

Soit le prédicat Cx (absence de parenthèses) qui signifie « x est un crayon de cire ». Comment pouvons-nous affirmer que tous les objets dans cette situation sont des crayons de cire?

Tous les crayons doivent être de cire.

Le langage Prédicat contient un symbole, ∀ qui signifie « tout ». C’est le quantificateur universel.

Il doit toujours être suivi d’une variable, par exemple ∀x et être mis entre parenthèses (∀x).

Nous pouvons alors écrire (∀x)Cx, ce qui signifie « tout x est un crayon de cire », ou encore « tout objet est un crayon de cire ».

Le quantificateur existentiel

Comment dire en prédicat qu’il y a au moins une pomme dans la toile de Chardin³?

Le symbole ∃ signifie « il existe » ou « il y a au moins un » ou « certains » ou encore « quelques ».

Il doit toujours être suivi d’une variable et être mis entre parenthèses :

(∃x)

Nous pouvons écrire (∃x)Px où Px signifie « x est une pomme ». L’énoncé se lit alors comme suit : « certains objets x sont des pommes » ou « il y a un objet x qui est une pomme » ou « quelques objets sont des pommes ».

Le choix de la variable employée ne change pas le sens de l’énoncé :

(∀x)Cx, (∀y)Cy, (∀x34)Cx34, etc.

Note : (∀x)Cy ne dit pas la même chose (deux variables différentes sont impliquées, x et y).

La notion de domaine et la généralité

Terminologie : un domaine ou un univers du discours pour un quantificateur est comme un ensemble d’objets qui sont visés par le discours.

Dans l’exemple de la toile de Janet Fish, ce sont des objets représentés⁴.

Soient les prédicats :

• F(x) : « x est un fruit »;
• P(x) : « x est dans un plat ».

Comment pouvons-nous affirmer :

Tous les fruits sont dans un plat.

?

Considérons la formule suivante :

Fy ⊃ Py

La formule ne comporte aucun quantificateur universel.

N.B. ce n’est pas une proposition. Elle n’est ni vraie ni fausse. La variable y dot être remplacée par un nom d’objet pour qu’elle devienne une proposition.

Divisons les objets en deux : les fruits et les non-fruits.

Non-fruits : Fa ⊃ Pa.

Fb ⊃ Pb, etc. Sont toutes vraies puisque l’antécédent est toujours faux.

Fruits : Fe ⊃ Pe, Ff ⊃ Pf, etc. sont vraies aussi.

Donc (∀y)(Fy ⊃ Py) est vraie dans cette situation (lorsqu’on teste la formule pour chaque élément : les fruits sont toujours dans des plats).

Pourquoi ne pas écrire :

(∀y)(Fy ∧ Py)

pour exprimer que tous les fruits sont dans des plats?

Cette formule est trop forte : elle concerne tous les éléments (pas seulement les fruits).

Soit le prédicat suivant :

• C(x) : « x est coupé ».

Comment dire que certains fruits sont coupés?

La formule Fy ∧ Cy signifie « y est un fruit et y est coupé ».

L’énoncé Fe ∧ Ce est vrai dans cette situation.

Il y a donc un objet qui est un fruit et qui est coupé dans cette situation.

Nous pouvons écrire, en Prédicat :

(Ex)(Fx ∧ Cx)

Cette formule exprime qu’il y a un objet qui est un fruit et cet objet est coupé.

Pourquoi pas :

(∃y)(Fy ⊃ Cy)

?

Parce que c’est trop faible : l’énoncé sera satisfait trop facilement, il serait vrai trop souvent; on trouvera un antécédent faux et un conséquent vrai; on trouvera des cas où c’est vrai et c’est faux.

Exemple 1 : les corbeaux noirs

Soit l’énoncé :

Tous les corbeaux sont noirs.

Dictionnaire :

• C(x) = x : « est un corbeau »;
• N(x) = x : « est noir ».

La traduction en LPO :

(∀x)(Cx ⊃ Nx)

On divise le monde entre les corbeaux et non-corbeaux; tout ce qui est corbeau est noir.

Induction : « Tous les a sont des b… » se traduit généralement par une implication (a ⊃ b).

Exemple 2 : le noir et les corbeaux

Soit l’énoncé :

Tout ce qui est noir est un corbeau.

Dictionnaire :

• N(x) : « x est noir »;
• C(x) : « x est un corbeau ».

Traduction de l’énoncé en LPO :

(∀x)(Nx ⊃ Cx)

Exemple 3 : les philosophes incompréhensibles et populaires

Soit l’énoncé :

Certains philosophes sont incompréhensibles et populaires.

• P(x) : « x est un philosophie »;
• I(x) : « x est incompréhensible »;
• Q(x) : « x est populaire ».

Traduction de l’énoncé en LPO :

(∃x)(Px ∧ (Ix ∧ Qx))

Exemple 4 : Coco et les corbeaux blancs

Soit l’énoncé :

Si Coco est un corbeau, alors il y a des corbeaux qui sont blancs.

Dictionnaire :

• C(x) : « x est un corbeau »;
• B(x) : « x est blanc »;
• c : Coco.

Traduction de l’énoncé en LPO :

C(c) ⊃ (∃x)(Cx ∧ Bx)

Exemple 5 : les vins et le sucre

Soit l’énoncé :

Tous les vins contiennent du sucre.

Dictionnaire :

• V(x) : « x est du vin »;
• S(x) : « x contient du sucre ».

Traduction de l’énoncé en LPO :

(∀x)(Vx ⊃ Sx)

Exemple 6 : choses certaines et choses probables

Soit l’énoncé :

S’il y a des choses certaines, il y a des choses probables.

Dictionnaire :

• C(x) : « x est certain »;
• P(x) : « x est probable ».

Traduction de l’énoncé en LPO :

(∃x)(Cx) ⊃ (∃x)(Px)

ou

(∃x)(Cx) ⊃ (∃y)(Py)

(ces deux formes sont logiquement équivalentes; la seule différence est syntaxique entre x et y dans la deuxième partie de la formule).

Notez bien

Les énoncés de la forme « Tous les P sont des Q » se traduisent en LPO de la manière suivante :

(∀x)(Px ⊃ Qx)

Les énoncés de la forme « Certains P sont des Q » ou « il existe des P qui sont des Q » se traduisent de la manière suivante :

(∃x)(Px ∧ Qx)

L’argument initial en LPO

L’argument initial :

1. Tous les humains sont des animaux;\
2. Certains humains sont des philosophes;\
3. Certains animaux sont des philosophes.

Dictionnaire :

• H(x) : « x est un humain »;
• A(x) : « x est un animal »;
• P(x) : « x est un philosophe ».

Traduction en LPO :

1. (∀x)(Hx ⊃ Ax)
2. (∃x)(Hx ∧ Px)
------
C. (∃x)(Ax ∧ Px)

Notes